Κανάλια επικοινωνίας:
Φυσικές δίοδοι, που επιτρέπουν σε σήματα κωδικοποιημένα μέσω μίας συγκεκριμένης φυσικής ποσότητας, να μεταδοθούν κατά μήκος τους. Κάθε κανάλι μπορεί να μεταδώσει, χωρίς σημαντικές απώλειες ισχύος, σήματα που περιέχουν συχνότητες μόνο εντός ενός συγκεκριμένου εύρους· αυτό είναι το εύρος ζώνης του καναλιού. Το φυσικό μέσο χάρη στις ιδιότητες του οποίου μεταδίδεται η πληροφορία, είναι τα ηλεκτρόνια (ηλεκτρισμός)και τα φωτόνια (φως και ηλεκτρομαγνητικό κύμα).
Μη-Τοπικότητα:
DNA το μόριο της ζωής
Το Πείραμα EPR, το πρώτο από τα επαναστατικά πειράματα που έδειξε την μη-τοπικότητα της μικροσφαίρας της φυσικής πραγματικότητας, διατυπώθηκε από τον A.Einstein και τους συνεργάτες του B. Podolskyι και N. Rosen το 1935. Σε αυτό το «πείραμα σκέψης» (που ονομάστηκε έτσι επειδή εκείνη την εποχή δεν μπορούσε να επαληθευτεί εμπειρικά) παίρνουμε δυο σωματίδια που βρίσκονται στη λεγόμενη μονήρη κατάσταση, στην οποία τα σπιν τους αντισταθμίζουν το ένα το άλλο δίνοντας μηδενικό συνολικό σπιν. Επιτρέπουμε στα σωματίδια να χωριστούν και να ταξιδέψουν μια πεπερασμένη απόσταση. Αν μπορούσαμε στην συνέχεια να μετρήσουμε τα σπιν και των δυο σωματιδίων, θα γνωρίζαμε την κατάστασή τους ταυτόχρονα. Ο Αϊνστάιν πίστευε ότι αυτό θα έδειχνε πως ο παράξενος περιορισμός που επιβάλλεται στις μετρήσεις από την αρχή της αβεβαιότητας του Χάιζενμπεργκ (Heisenberg) τελικά δεν ισχύει. Η θεωρία στην οποία βασίζεται δεν παρέχει μια πλήρη περιγραφή της φυσικής πραγματικότητας. Όταν επινοήθηκαν πειραματικές συσκευές αρκετά εξελιγμένες για να ελέγξουν αν ο Αϊνστάιν είχε δίκιο, αποδείχτηκε ότι δεν συμβαίνει αυτό ακριβώς που αναμενόταν. Ας υποθέσουμε ότι μετρούμε το σπιν του ενός σωματιδίου-του σωματιδίου Α- κατά μήκος κάποιας κατεύθυνσης, ας πούμε κατά τον άξονα z (οι επιτρεπόμενες καταστάσεις σπιν είναι προς τα «πάνω» ή προς τα «κάτω» κατά τους άξονες χ, ψ και z). Ας πούμε ότι η μέτρηση δείχνει πως το σπιν είναι στην κατεύθυνση «πάνω». Επειδή τα σπιν των σωματιδίων πρέπει να αντισταθμίζουν το ένα το άλλο, το σπιν του σωματιδίου Β πρέπει να είναι «κάτω». Όμως τα σωματίδια απέχουν μεταξύ τους και αυτή η προϋπόθεση δεν θα έπρεπε να ισχύει. Ισχύει όμως. Κάθε μέτρηση του ενός σωματιδίου δίνει ένα συμπληρωματικό αποτέλεσμα στη μέτρηση του άλλου. Φαίνεται ότι η μέτρηση του σωματιδίου Α έχει ακαριαία επίδραση πάνω στο Β, κάνοντας την κυματοσυνάρτηση του σπιν του να καταρρεύσει στη συμπληρωματική κατάσταση. Η μέτρηση του Α δεν αποκαλύπτει απλώς μια ήδη εδραιωμένη κατάσταση στο Β: στην πραγματικότητα παράγει αυτή την κατάσταση. Μια ακαριαία επίδραση μεταδίδεται από το Α στο Β, μεταφέροντας ακριβείς πληροφορίες για αυτό που μετράται. Το Β «γνωρίζει» πότε μετράται το Α, για ποια παράμετρο και με ποιο αποτέλεσμα, αφού περνά κι αυτό στη δική του αντίστοιχη κατάσταση. Μια μη τοπική σύνδεση συνδέει το Α και το Β, παρ’ όλη την απόσταση που τα χωρίζει.
Πειράματα που έγιναν στη δεκαετία του 1980 από τον Αλαίν Ασπέ (Alain Aspect) και τους συνεργάτες του, και επαναλήφθηκαν από τον Νίκολας Γκίζιν (Nicolas Gisin) το 1997, δείχνουν ότι η ταχύτητα με την οποία μεταδίδεται το φαινόμενο είναι ασύλληπτη. Στα πειράματα του Ασπέ η επικοινωνία ανάμεσα σε σωματίδια που απέχουν δώδεκα μέτρα εκτιμήθηκε ότι χρειάστηκε λιγότερο από ένα δισεκατομμυριοστό του δευτερολέπτου, δηλαδή ήταν γύρω στις είκοσι φορές μεγαλύτερη από την ταχύτητα του φωτός στον άδειο χώρο, και στο πείραμα του Γκίζιν σωματίδια που απείχαν δέκα χιλιόμετρα εμφανίστηκαν να επικοινωνούν 20.000 φορές ταχύτερα από την ταχύτητα του φωτός, το υποτιθέμενο απαραβίαστο όριο ταχύτητας της θεωρίας της σχετικότητας. Τα πειράματα δείχνουν επίσης ότι η σύνδεση ανάμεσα στα σωματίδια δεν μεταδίδεται με συμβατικά μέσα διαμέσου της συσκευής μέτρησης, αλλά είναι ένα εγγενές χαρακτηριστικό των ίδιων των σωματιδίων. Τα σωματίδια είναι «διαπλεγμένα» (συζευγμένα) μεταξύ τους: η συσχέτισή τους δεν είναι ευαίσθητη ούτε στην απόσταση ούτε στη διαφορά χρόνου. Μεταγενέστερα πειράματα περιλάμβαναν περισσότερα σωματίδια σε όλο και μεγαλύτερες αποστάσεις μεταξύ τους, χωρίς να αλλάξουν αυτά τα απρόσμενα αποτελέσματα. Φαίνεται ότι η απόσταση δεν χωρίζει τα σωματίδια μεταξύ τους-αλλιώς η μέτρηση του ενός δεν θα προκαλούσε αλλαγή στο άλλο. Δεν είναι καν απαραίτητο να έχουν αρχικά τα σωματίδια την ίδια κβαντική κατάσταση. Πειράματα έδειξαν ότι δυο οποιαδήποτε σωματίδια (ανεξάρτητα αν είναι ηλεκτρόνια, νετρόνια ή φωτόνια), που προέρχονται από διαφορετικά σημεία του χώρου και του χρόνου, αν ενωθούν μια φορά μέσα στο ίδιο σύστημα συντεταγμένων, αυτό είναι αρκετό για να συνεχίσουν να ενεργούν ως μέρη του ίδιου κβαντικού συστήματος ακόμη και αφού διαχωριστούν.
(Απόσπασμα απο το βιβλίο του Ervin Lazlo “Η νέα επιστήμη και το ακασικό πεδίο“ εκδ.Αρχέτυπο)
Fractal:
Με τον διεθνή όρο φράκταλ (fractal, ελλ. μορφόκλασμα ή μορφοκλασματικό σύνολο) στα Μαθηματικά, τη Φυσική αλλά και σε πολλές επιστήμες ονομάζεται ένα γεωμετρικό σχήμα που επαναλαμβάνεται αυτούσιο σε άπειρο βαθμό μεγέθυνσης, κι έτσι συχνά αναφέρεται σαν “απείρως περίπλοκο”. Το φράκταλ παρουσιάζεται ως “μαγική εικόνα” που όσες φορές και να μεγεθυνθεί οποιοδήποτε τμήμα του θα συνεχίζει να παρουσιάζει ένα εξίσου περίπλοκο σχέδιο με μερική ή ολική επανάληψη του αρχικού. Χαρακτηριστικό επομένως των φράκταλ είναι η λεγόμενη αυτο-ομοιότητα (self-similarity) σε κάποιες δομές τους, η οποία εμφανίζεται σε διαφορετικά επίπεδα μεγέθυνσης.
(Πηγή: Βικιπαίδεια)
Πειράματα Τηλεμεταφοράς:
Πρόσφατα πειράματα δείχνουν ότι μια μορφή μη τοπικής σύνδεσης που είναι γνωστή ως «τηλεμεταφορά» υπάρχει όχι μόνο ανάμεσα σε μεμονωμένα σωματίδια, αλλά ακόμη και ανάμεσα σε ολόκληρα άτομα. Η τηλεμεταφορά αποδείχτηκε πειραματικά το 1997 για την κβαντική κατάσταση φωτονίων σε δέσμες φωτός και για την κατάσταση των μαγνητικών πεδίων που παράγονται από νέφη ατόμων. Την άνοιξη του 2004 πειράματα-ορόσημα από δυο ομάδες φυσικών, μία στο Εθνικό Ινστιτούτο Μέτρων και Σταθμών στο Κολοράντο και μία στο Πανεπιστήμιο του Ίνσμπουργκ στην Αυστρία, έδειξαν ότι η κβαντική κατάσταση ολόκληρων ατόμων μπορεί να τηλεμεταφερθεί με τη μεταφορά κβαντικών bits («qubits») που ορίζουν τα άτομα. Στο πείραμα του Κολοράντο, με επικεφαλής τον Μ. Ντ. Μπάρετ (M.D. Barret), τηλεμεταφέρθηκε με επιτυχία η βασική κατάσταση ιόντων βηρυλλίου, και στο πείραμα του Ίνσμπρουκ, με επικεφαλής τον Μ. Ριμπ (M. Riebe), τηλεμεταφέρθηκαν οι βασικές και μετασταθερές καταστάσεις μαγνητικά παγιδευμένων ιόντων ασβεστίου. Οι φυσικοί πέτυχαν μια τηλεμεταφορά με εξαιρετικά υψηλή πιστότητα-78% από την ομάδα του Κολοράντο και 75% από την ομάδα του Ίνσμπουργκ-χρησιμοποιώντας διαφορετικές τεχνικές αλλά ακολουθώντας το ίδιο βασικό πρωτόκολλο.

Arabidopsis thaliana: Αραβιδόψις η ταλιανή, ένα ζιζάνιο σινάπεως, αποτελεί ένα από τα πρώτα φυτά του οποίου το γονιδίωμα κωδικοποιήθηκε.
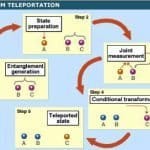
Πρώτα, δυο φορτισμένα άτομα (ιόντα), που ονομάζονται Α και Β, «διαπλέκονται», δημιουργώντας την ακαριαία σύνδεση που παρατηρείται και στο πείραμα EPR. Κατόπιν, κωδικοποιείται μέσα σε ένα τρίτο άτομο, που ονομάζεται Ρ, η σύμφωνη υπερτιθέμενη κβαντική κατάσταση που θα τηλεμεταφερθεί. Κατόπιν μετράται το Α, ένα από τα διαπλεγμένα όντα, και το άτομο Ρ. Σε αυτό το σημείο η εσωτερική κβαντική κατάσταση του Β μετασχηματίζεται, και παίρνει ακριβώς την κατάσταση που είχε κωδικοποιηθεί μέσα στο Ρ!. Δηλαδή, η κβαντική κατάσταση του Ρ «τηλεμεταφέρεται» στο Β. Αν και τα πειράματα απαιτούν πολύπλοκες διεργασίες, η φυσική διαδικασία που επιδεικνύουν είναι σχετικά απλή. Όταν το Α και το Ρ μετρηθούν μαζί, η προϋπάρχουσα μη τοπική σύνδεση ανάμεσα στο Α και το Β δημιουργεί μια μη τοπική μεταφορά κατάστασης από το Ρ στο Β. Στο πείραμα EPR, το ένα από τα δυο διαπλεγμένα σωματίδια «πληροφορεί διαμορφωτικά» ή «δια-πληροφορεί» το άλλο για τη μετρηθείσα κατάστασή του. Παρόμοια, στα πειράματα τηλεμεταφοράς, η μέτρηση του ενός από τα δυο διαπλεγμένα ιόντα μαζί με ένα τρίτο τον κωδικοποιεί στην κατάσταση του τρίτου ιόντος στο δεύτερο δίδυμο ιόν. Επειδή η διαδικασία καταστρέφει την υπερτιθέμενη κβαντική κατάσταση του Α και την αναδημιουργεί στο Ρ, θυμίζει την ιδέα της «τηλεμεταφοράς» ενός αντικειμένου από ένα σημείο σε ένα άλλο, η οποία απαντάται στην επιστημονική φαντασία. Τα πιο εξελιγμένα πειράματα τηλεμεταφοράς ανοίγουν τεράστιους ορίζοντες. Σε λίγο οι φυσικοί θα βρουν τρόπους για να τηλεμεταφέρουν qubits όχι μόνο από ένα άτομο σε ένα άλλο, αλλά ανάμεσα σε ένα μεγάλο αριθμό σωματιδίων ταυτόχρονα. Αυτό θα οδηγήσει σε διάφορες τεχνολογικές καινοτομίες, ανάμεσα τους και μια νέα γενιά ταχύτατων κβαντικών υπολογιστών. Αν διανεμηθεί ένας μεγάλος αριθμός διαπλεγμένων σωματιδίων σε όλη τη δομή ενός υπολογιστή, η «κβαντική τηλεμεταφορά» μπορεί να δημιουργήσει μια ακαριαία μεταφορά πληροφοριών ανάμεσα τους χωρίς να χρειάζεται να συνδέονται τα σωματίδια μεταξύ τους ή ακόμη και να είναι το ένα δίπλα στο άλλο.
(Απόσπασμα απο το βιβλίο του Ervin Lazlo “Η νέα επιστήμη και το ακασικό πεδίο“ εκδ.Αρχέτυπο)
Μνήμη του εγκεφαλικού φλοιού:
Ο αυστριακός ψυχολόγος Karl H. Pribram καθηγητής στα πανεπιστήμια Stanford, Yale, κατέληξε στο ολογραφικό μοντέλο (Ολονομική Θεωρία Εγκεφάλου) ερευνώντας το πως αποθηκεύεται η μνήμη στον εγκέφαλο. Οι έρευνές του έδειξαν ότι η μνήμη δεν περιορίζεται σε συγκεκριμένα τμήματα αλλά είναι κατανεμημένη σε ολόκληρο τον εγκέφαλο. Σε προηγούμενα πειράματα του ο Karl Lashley (αμερικανός ψυχολόγος γνωστός για τις έρευνές του στο τομέα της μνήμης και μάθησης) σε ποντικούς διαπίστωσε πως οποιοδήποτε τμήμα του εγκεφάλου κι αν αφαιρείτο ήταν αδύνατο να σβηστεί η μνήμη που αφορούσε την εκτέλεση πολύπλοκων λειτουργιών. Οταν στην δεκαετία του 1960 ο Pribram ήρθε σε επαφή με την ολογραφία συνειδητοποίησε πως είχε βρει τον χαμένο κρίκο. Οτι η μνήμη δεν κωδικοποιείται στους νευρώνες αλλά σε πρότυπα νευρικών παλμών που διατρέχουν τον εγκέφαλο με τον ιδιο τρόπο που πρότυπα παρεμβολής του φωτός διατρέχουν ολόκληρη την επιφάνεια ενός φίλμ που περιέχει μία ολογραφική εικόνα. Για τον Pribram και άλλους πλέον επιστήμονες, ο ίδιος ο εγκέφαλος θεωρείται ως ολόραμμα κι έτσι εξηγείται η τεράστια ικανότητα και χωρητικότητα πληροφορίας σε ένα τόσο μικρό χώρο.
Ολόγραμμα:
Ένα ολόγραμμα είναι μια τρισδιάστατη φωτογραφία που γίνεται με τη βοήθεια ενός λέιζερ. Για να γίνει ένα ολόγραμμα, η φωτογραφική πλάκα φωτίζεται από μια δέσμη λέιζερ. Παράλληλα. μια δεύτερη δέσμη ακτίνων λέιζερ φωτίζει το υπό φωτογράφηση αντικείμενο και το ανακλώμενο φως της πέφτει κι αυτό στη φωτογραφική πλάκα. Το πρότυπο παρεμβολής (η ανάμειξη δηλαδή των δύο ακτίνων λέιζερ) αιχμαλωτίζεται έτσι στη πλάκα. Όταν εμφανιστεί το φιλμ, αυτό που φαίνεται είναι ένας ακατανόητος στρόβιλος φωτεινών και σκοτεινών γραμμών. Μόλις όμως το φιλμ φωτιστεί από μια άλλη δέσμη λέιζερ, εμφανίζεται μια τρισδιάστατη εικόνα του αρχικού αντικειμένου.

Ολογραφική εικόνα: Μπορείτε να πλησιάσετε την εικόνα, περίπου στα 30 εκ. εστιάζοντας με έναν τρόπο σαν να κοιτάτε πίσω και πέρα από αυτήν. Έτσι θα αναδυθεί μπροστά σας το κρυμμένο μοτίβο. Χρειάζεται λίγη εξάσκηση.
Το τρισδιάστατο αυτών των εικόνων δεν είναι το μόνο αξιόλογο χαρακτηριστικό των ολογραμμάτων. Αν το ολόγραμμα ενός τριαντάφυλλου κοπεί στη μέση και ύστερα φωτιστεί από ένα λέιζερ, το κάθε μισό θα συνεχίσει να περιέχει ολόκληρη την εικόνα του τριαντάφυλλου. Μάλιστα, ακόμα και αν τα δύο μισά ξανακοπούν στη μέση, κάθε κομμάτι του φιλμ θα περιέχει πάντοτε μια μικρότερη αλλά πλήρη εκδοχή της αρχικής εικόνας. Αντίθετα από την κανονική φωτογραφία, κάθε κομμάτι του ολογράμματος περιέχει όλες τις πληροφορίες που διαθέτει το σύνολο. Η φύση της ολογραφίας (το όλον σε κάθε τμήμα) μας προσφέρει έναν εντελώς καινούργιο τρόπο να κατανοήσουμε την οργάνωση και την τάξη. Στη μεγαλύτερη διάρκεια της ιστορίας της, η δυτική επιστήμη έχει κινηθεί με την αντίληψη ότι ο καλύτερος τρόπος να κατανοήσουμε ένα φυσικό φαινόμενο, είτε πρόκειται για ένα βάτραχο είτε για ένα άτομο, είναι να το τεμαχίσουμε και να μελετήσουμε τα τμήματά του. Η ολογραφία μας διδάσκει ότι μερικά πράγματα στο σύμπαν μάλλον δεν προσφέρονται γι’ αυτή την προσέγγιση. Αν προσπαθήσουμε να τεμαχίσουμε κάτι που έχει κατασκευαστεί ολογραφικά, δεν θα πάρουμε τα τμήματα που το απαρτίζουν, αλλά μόνο μικρότερα σύνολα. Ο φυσικός David Bohm του Πανεπιστημίου του Λονδίνου, προτείνει την εξής εικόνα. Φαντασθείτε ένα ενυδρείο που περιέχει ένα ψάρι. Φαντασθείτε επίσης ότι δεν μπορείτε να δείτε κατευθείαν το ενυδρείο και ότι η γνώση σας γι’ αυτό και για όσα περιέχει προέρχεται από δύο τηλεοπτικές κάμερες, που η μια βλέπει την πρόσοψη του ενυδρείου και η άλλη το πλάι του. Καθώς κοιτάτε τις δύο τηλεοπτικές οθόνες, αρχικά μάλλον θα υποθέσετε ότι το ψάρι σε κάθε οθόνη είναι μια ιδιαίτερη οντότητα. Αφού οι κάμερες βλέπουν από διαφορετικές γωνίες, κάθε εικόνα θα είναι αρκετά διαφορετική. Αλλά καθώς συνεχίζετε να κοιτάτε τα δύο ψάρια, κάποια στιγμή θα αντιληφθείτε ότι υπάρχει μια συγκεκριμένη σχέση ανάμεσά τους: Όταν το ένα ψάρι γυρίζει, το άλλο κάνει επίσης μια ελαφρώς διαφορετική αλλά αντίστοιχη στροφή. Όταν το ένα κοιτάζει μπροστά, το άλλο πάντοτε κοιτάζει προς το πλάι. Κι ενώ μοιάζει να πρόκειται για δύο διαφορετικές οντότητες στην πραγματικότητα πρόκειται για μία και την αυτή. Ο Bohm πιστεύει ότι ο λόγος που τα υποατομικά σωματίδια μπορούν να επικοινωνούν μεταξύ τους ανεξάρτητα από την απόσταση που τα χωρίζει δεν είναι ότι στέλνουν πέρα δώθε κάποιου είδους μυστηριώδη μηνύματα, αλλά επειδή η χωριστότητά τους είναι μια ψευδαίσθηση. Υποστηρίζει ότι σε κάποιο βαθύτερο επίπεδο πραγματικότητας τα σωματίδια αυτά δεν είναι ιδιαίτερες οντότητες, αλλά προεκτάσεις του ίδιου θεμελιακού όντος.

Σολιτονικό κύμα ταξιδεύει προς την ακτή ενός νησιού της Χαβάης
Γονιδίωμα:
Είναι το σύνολο του γενετικού υλικού που βρίσκεται σε ένα κύτταρο. Στους ευκαρυωτικούς οργανισμούς όπως το ανθρώπινο σώμα, ο όρος αναφέρεται στο γενετικό υλικό του κυτταρικού πυρήνα.
Σολιτονικά κύματα:
Εντοπισμένα μοναδικά κυματοπακέτα με μορφή αναλλοίωτη η περιοδικά μεταβαλλόμενη. Δημιουργούνται από την αμοιβαία εξισορρόπηση φαινομένων. Δεν μεταβάλλουν το πλάτος, την ενέργεια, η την ταχύτητα τους μετά από συγκρούσεις με άλλα κύμματα, παραμένουν αναλλοίωτα σαν σωματίδια εξ’ ου και ο όρος “soliton”: μοναδικό. Έχουν δυαδική φύση, σωματιδιακή και κυματική. Είναι μη γραμμικές οντότητες. Λόγω της σταθερότητας τους μπορούν να αποθηκεύσουν για κάποιο χρονικό διάστημα, πληροφορία.